23 Image Visualization and output

Chapter 23
Image Visualization and output

After processing your images with OTB, you probably want to see the result. As it is quite straightforward in some situation, if can be a bit trickier in other. For example, some filters will give you a list of polygons as an output. Other can return an image with each region labelled by a unique index. In this section we are going to provide few examples to help you produce beautiful output ready to be included in your publications/presentations.

23.1 Images

23.1.1 Grey Level Images

The source code for this example can be found in the file
Examples/BasicFilters/ScalingFilterExample.cxx.

On one hand, satellite images are commonly coded on more than 8 bits to provide the dynamic range required from shadows to clouds. On the other hand, image formats in use for printing and display are usually limited to 8 bits. We need to convert the value to enable a proper display. This is usually done using linear scaling. Of course, you have to be aware that some information is lost in the process.

The itk::RescaleIntensityImageFilter is used to rescale the value:

    typedef itk::RescaleIntensityImageFilter<InputImageType,
        OutputImageType> RescalerType;
    RescalerType::Pointer rescaler = RescalerType::New();
    rescaler->SetInput(reader->GetOutput());

Figure 23.1 illustrates the difference between a proper scaling and a simple truncation of the value and demonstrates why it is important to keep this in mind.

Figure 23.1: On the left, the image obtained by truncated pixel values at the dynamic acceptable for a png file (between 0 and 255). On the right, the same image with a proper rescaling

23.1.2 Multiband Images

The source code for this example can be found in the file
Examples/BasicFilters/PrintableImageFilterExample.cxx.

Most of the time, satellite images have more than three spectral bands. As we are only able to see three colors (red, green and blue), we have to find a way to represent these images using only three bands. This is called creating a color composition.

Of course, any color composition will not be able to render all the information available in the original image. As a consequence, sometimes, creating more than one color composition will be necessary.

If you want to obtain an image with natural colors, you have to match the wavelength captured by the satellite with those captured by your eye: thus matching the red band with the red color, etc.

Some satellites (SPOT 5 is an example) do not acquire all the human spectral bands: the blue can be missing and replaced by some other wavelength of interest for a specific application. In these situations, another mapping has to be created. That’s why, the vegetation often appears in red in satellite images (see on left of figure 23.2).

The band order in the image products can be also quite tricky. It could be in the wavelength order, as it is the case for Quickbird (1: Blue, 2: Green, 3: Red, 4: NIR), in this case, you have to be careful to reverse the order if you want a natural display. It could also be reverse to facilitate direct viewing, as for SPOT5 (1: NIR, 2: Red, 3: Green, 4: SWIR) but in this situations you have to be careful when you process the image.

To easily convert the image to a printable format, i.e. 3 bands unsigned char value, you can use the otb::PrintableImageFilter .

    typedef otb::PrintableImageFilter<InputImageType> PrintableFilterType;
    PrintableFilterType::Pointer printableImageFilter = PrintableFilterType::New();

    printableImageFilter->SetInput(reader->GetOutput());
    printableImageFilter->SetChannel(redChannelNumber);
    printableImageFilter->SetChannel(greenChannelNumber);
    printableImageFilter->SetChannel(blueChannelNumber);

When you create the writer to plug at the output of the printableImageFilter you may want to use the direct type definition as it is a good way to avoid mismatch:

typedef PrintableFilterType::OutputImageType OutputImageType;
typedef otb::ImageFileWriter<OutputImageType> WriterType;

Figure 23.2 illustrates different color compositions for a SPOT 5 image.

Figure 23.2: On the left, a classic SPOT5 combination: XS3 in red, XS2 in green and XS1 in blue. On the right another composition: XS3 in red, XS4 in green and XS2 in blue.

23.1.3 Indexed Images

The source code for this example can be found in the file
Examples/BasicFilters/IndexedToRGBExample.cxx.

Some algorithms produce an indexed image as output. In such images, each pixel is given a value according to the region number it belongs to. This value starting at 0 or 1 is usually an integer value. Often, such images are produced by segmentation or classification algorithms.

If such regions are easy to manipulate – it is easier and faster to compare two integers than a RGB value – it is different when it comes to displaying the results.

Here we present a convient way to convert such indexed image to a color image. In such conversion, it is important to ensure that neighborhood region, which are likely to have consecutive number have easily dicernable colors. This is done randomly using a hash function by the itk::ScalarToRGBPixelFunctor .

The itk::UnaryFunctorImageFilter is the filter in charge of calling the functor we specify to do the work for each pixel. Here it is the itk::ScalarToRGBPixelFunctor .

    typedef itk::Functor::ScalarToRGBPixelFunctor<unsigned long>
    ColorMapFunctorType;
    typedef itk::UnaryFunctorImageFilter<ImageType, RGBImageType,
        ColorMapFunctorType> ColorMapFilterType;
    ColorMapFilterType::Pointer colormapper = ColorMapFilterType::New();

    colormapper->SetInput(reader->GetOutput());

Figure 23.3 shows the result of the conversion from an indexed image to a color image.

Figure 23.3: The original indexed image (left) and the conversion to color image.

23.1.4 Altitude Images

The source code for this example can be found in the file
Examples/BasicFilters/DEMToRainbowExample.cxx.

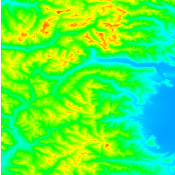
In some situation, it is desirable to represent a gray scale image in color for easier interpretation. This is particularly the case if pixel values in the image are used to represent some data such as elevation, deformation map, interferogram. In this case, it is important to ensure that similar values will get similar colors. You can notice how this requirement differs from the previous case.

The following example illustrates the use of the otb::DEMToImageGenerator class combined with the otb::ScalarToRainbowRGBPixelFunctor . You can refer to the source code or to section 7.1 for the DEM conversion to image, we will focus on the color conversion part here.

As in the previous example, the itk::ScalarToRGBColormapImageFilter is the filter in charge of calling the functor we specify to do the work for each pixel. Here it is the otb::ScalarToRainbowRGBPixelFunctor .

    typedef itk::ScalarToRGBColormapImageFilter<ImageType,
        RGBImageType> ColorMapFilterType;
    ColorMapFilterType::Pointer colormapper = ColorMapFilterType::New();
    colormapper->UseInputImageExtremaForScalingOff();

    if (argc == 9)
      {
      typedef otb::Functor::ScalarToRainbowRGBPixelFunctor<PixelType,
          RGBPixelType>
      ColorMapFunctorType;
      ColorMapFunctorType::Pointer colormap = ColorMapFunctorType::New();
      colormap->SetMinimumInputValue(0);
      colormap->SetMaximumInputValue(4000);
      colormapper->SetColormap(colormap);
      }

And we connect the color mapper filter with the filter producing the image of the DEM:

colormapper->SetInput(demToImage->GetOutput());

Figure 23.4 shows the effect of applying the filter to a gray scale image.

Figure 23.4: The gray level DEM extracted from SRTM data (top-left) and the same area represented in color.

The source code for this example can be found in the file
Examples/BasicFilters/HillShadingExample.cxx.

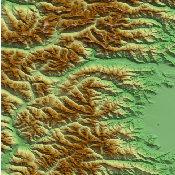
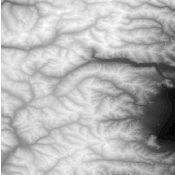
Visualization of digital elevation models (DEM) is often more intuitive by simulating a lighting source and generating the corresponding shadows. This principle is called hill shading.

Using a simple functor otb::HillShadingFunctor and the DEM image generated using the otb::DEMToImageGenerator (refer to 7.1), you can easily obtain a representation of the DEM. Better yet, using the otb::ScalarToRainbowRGBPixelFunctor , combined with the otb::ReliefColormapFunctor you can easily generate the classic elevation maps.

This example will focus on the shading itself.

After generating the DEM image as in the DEMToImageGenerator example, you can declare the hill shading mechanism. The hill shading is implemented as a functor doing some operations in its neighborhood. A convenient filter called otb::HillShadingFilter is defined around this mechanism.

    typedef otb::HillShadingFilter<ImageType, ImageType> HillShadingFilterType;
    HillShadingFilterType::Pointer hillShading = HillShadingFilterType::New();
    hillShading->SetRadius(1);
    hillShading->SetInput(demToImage->GetOutput());

Figure 23.5 shows the hill shading result from SRTM data.

Figure 23.5: Hill shading obtained from SRTM data (left) and combined with the color representation (right)

[prev] [prev-tail] [front] [up]